Landschaftsarchäologische Analysen im Bergischen Land
Das Bergische Land
Östlich von Köln liegt das Bergische Land, eine Mittelgebirgsregion mit vergleichsweise regenreichem und kühlen Klima und für den Ackerbau weniger geeigneten Böden. Diese natürlichen Gegebenheiten führten dazu, dass eine intensivere Besiedlung des Bergischen Landes erst im Mittelalter einsetzte. Deshalb besteht die Möglichkeit, mit Rechenverfahren erzielte Ergebnisse zur Siedlungsgeschichte mit den historischen Quellen zu vergleichen und so die verwendeten Methoden zu prüfen und weiter zu entwickeln. Hilfreich sind in diesem Zusammenhang gut dokumentierte alte Handelsrouten (Nicke 2001) und die Erstnennungen von Orten aus 16 Gemeinden dieser Region (Pampus 1998).
Umfeldanalysen
Immer mehr Archäologen nutzen Geographische Informationssysteme (GIS), um archäologische Fundstellen, Befunde und Funde zu verwalten, deren Verbreitung zu visualisieren und um den Raumbezug der archäologischen Relikte zu analysieren (z.B. Posluschny 2010). Die Umfeldanalyse ist ein Beispiel für eine solche GIS-Auswertung: In den ersten Umfeldanalysen wurde ein kreisförmiges Gebiet um jede Siedlungsstelle in Bezug auf gewisse Standortfaktoren untersucht. Ist für fast jede Siedlungsstelle die Bodengüte in einem solchen Umfeld hoch, obwohl im Untersuchungsgebiet schlechter Boden weit verbreitet ist, so liegt die Vermutung nahe, dass die Siedler guten Boden bevorzugten.
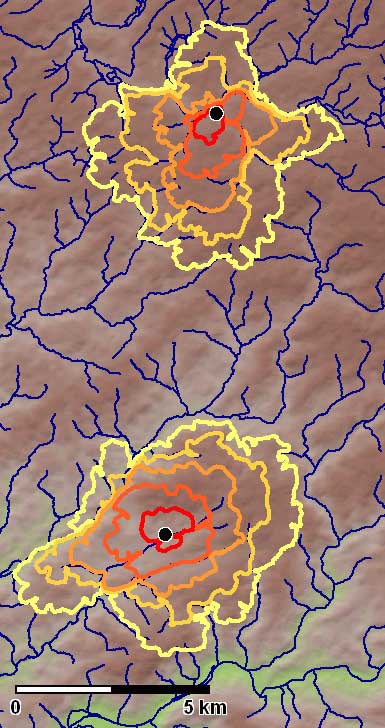
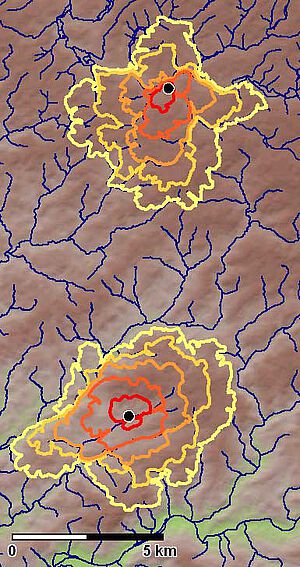
In den letzten Jahren hat sich eine andere Form der archäologischen Umfeldanalyse etabliert (s. Abb. 2): Dabei wird ausgehend von einem Punkt der Bereich abgegrenzt, der sich in einer vorgegebenen Zeit (meist eine Stunde) erreichen lässt (z.B. Posluschny 2010). Anders als bei den ersten Umfeldanalysen sind die so erzeugten Umfelder nicht mehr gleich groß. Bei der Auswertung sind dann sowohl die Größe eines solchen Umfeldes als auch die geographischen Gegebenheiten innerhalb dieses Bereiches zu berücksichtigen. So wird eine Siedlungsstelle mit vergleichsweise großem Umfeld mit hoher Bodengüte eher durch den Ackerbau geprägt sein als eine andere Stelle, die nur ein kleines Umfeld mit schlechtem Boden aufweist.
Abbildung 2 zeigt Beispiele für solche Umfelder, wobei für jeden der beiden betrachteten Siedlungspunkte Umfelder mit unterschiedlichen Radien ermittelt wurden. Für eine solche Form der Umfeldanalyse benötigt man ein Kostenmodell um abzuschätzen, wie hoch der Aufwand ist, um in einer vorgegebenen Landschaft voranzukommen. Ein solches Kostenmodell wird im Folgenden für das hier betrachtete Gebiet entwickelt. Eine genaue Diskussion von Abbildung 2 erfolgt dann im Anschluss.
Das Kostenmodell für Umfeldanalysen
Im Kostenmodell kann der Aufwand in Zeit (z.B. Stunden) oder in Energieverbrauch (z.B. Joule) gemessen werden. Zunächst stellt sich die Frage, welche Kostenfaktoren in das Kostenmodell integriert werden sollen und auch, wie diese zu kombinieren sind. Dabei ist es ratsam, das Kostenmodell zu überprüfen und gegebenenfalls zu verfeinern. Dies ist dann möglich, wenn der Streckenverlauf alter Handelsrouten im Untersuchungsgebiet bekannt ist. Grundlage solcher Analysen ist die Annahme, dass sich die Bewegungsmuster früherer Zeiten in den alten Handelsrouten erhalten haben.
Eine weitere Annahme ist, dass solche Altwege möglichst effektiv sind, also unnötige Aufwände vermeiden. Dies trifft vermutlich nicht für alle Altwege zu, Prozessionsstraßen und die Wege eines Schafhirten folgen sicherlich anderen Regeln. Aber bei häufig genutzten Handelswegen ist davon auszugehen, dass sich im Laufe der Zeit die effektivste Route durchgesetzt hat. Denn ein Händler, der von seinem Konkurrenten regelmäßig überholt wird, bleibt auf lange Sicht buchstäblich auf der Strecke. Damit ist zu erwarten, dass die alten Handelsrouten möglichst effektive Verbindungen im Sinne des noch zu ermittelnden Kostenmodells sind. Dabei können bei Bedarf auch kulturelle Faktoren in das Kostenmodell aufgenommen werden, z.B. das Bedürfnis, einen bestimmten Berggipfel möglichst lange im Blick zu behalten oder Bestattungsplätze zu meiden.
Optimale Wege
Wie im vorherigen Abschnitt erläutert, sollten alte Handelsrouten in der Regel einem möglichst effektivem, also einem optimalen Weg im Sinne des Kostenmodells entsprechen. Die ersten archäologischen Studien zur Berechnung optimaler Wege sind bereits vor ungefähr 20 Jahren erschienen. In den letzten zehn Jahren gibt es solche Studien mit zunehmender Häufigkeit, da die dafür benötigte GIS-Software inzwischen in vielen archäologischen Institutionen genutzt wird (z.B. Barbe 2007; Eichfeld 2005; Polla 2009). Ziel der Berechnungen ist meist, das Netzwerk der Wegeverbindungen zwischen Orten gleicher Zeitstellung zu rekonstruieren. Häufig sind alte Trassen in Abschnitten durch Luftbildbefunde oder andere archäologische Maßnahmen dokumentiert, dies erlaubt eine Überprüfung der Rechenergebnisse (s. Abb. 3). Fehlen solche Möglichkeiten zur Validierung, ist die Wahrscheinlichkeit eher gering, dass die errechneten Routen mit den tatsächlichen übereinstimmen.
Hinzu kommt, dass die meisten GIS-Programme zur Berechnung von optimalen Wegen Nachteile aufweisen. Der errechnete Weg setzt sich aus Einzelschritten zusammen, wobei in fast allen Programmen nur acht Bewegungsrichtungen vorgesehen sind. Dadurch kann der errechnete Weg bis zu 8,2 % länger werden als der tatsächlich optimale Weg, außerdem beträgt schlimmstenfalls der Abstand zwischen optimaler und errechneter Route 20% der Weglänge. Durch Erhöhung der Zahl der Bewegungsrichtungen können sowohl der Längen- als auch der Abstandsfehler erheblich reduziert werden, allerdings nimmt auch die Rechenzeit zu.
Auf und ab
Fast alle archäologischen Studien mit Wegeberechnungen berücksichtigen die Hangneigung. Es gehört zur Erfahrung jedes Wanderers, dass steile Anstiege anstrengender sind und häufig mehr Zeit kosten als eine flache Strecke auf vergleichbarem Untergrund. Doch eine solche qualitative Aussage reicht für Berechnungen nicht aus. Es ist eine Funktion erforderlich, die abhängig von der Hangneigung realistische Schätzungen für die Kosten, also den Energieverbrauch oder die benötigte Zeit liefert. Bei den hier vorgestellten Beispielen kommen zwei neuere Funktionen zum Einsatz, es wird unterschieden zwischen den Wegekosten von Fußgängern und Wagen.
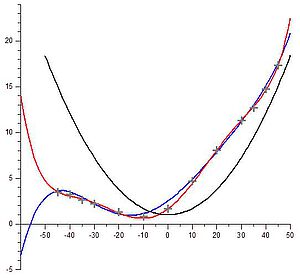
Die Kostenfunktion für den Energieverbrauch von Fußgängern beruht auf von Minetti et al. (2002) ermittelten physiologischen Messdaten, liefert jedoch bessere Schätzwerte als die von dieser Forschergruppe vorgeschlagene Kurve (s. Abb. 4):
f(s) = 1337,8 s[6] + 278,19 s[5] – 517,39 s[4] – 78,199 s[3] + 93,419 s[2] + 19,825 s + 1,64
wobei s die Hangneigung bezeichnet, und zwar gemessen in Höhendifferenz geteilt durch Länge der Strecke auf der Karte.
Die Ungenauigkeiten der von Minetti et al. (2002) vorgestellten Kurve sind evtl. noch tolerierbar, nicht jedoch die Tatsache, dass die Funktion für sehr steile Gefälle negative Werte annimmt; dies widerspricht der Erfahrung, benötigt doch jeder Schritt Energie und Zeit.
Die oben angesprochenen Messwerte und die daraus abgeleitete Funktion beziehen sich nur auf Fußgänger. Für Reittiere, Packtiere oder Wagen gelten andere Bedingungen. Es ist davon auszugehen, dass der Transport von schweren Lasten (Eisenstraße!) in Mittelalter und früher Neuzeit vielfach auf Wagen erfolgte. Meines Wissens sind Kostenfunktionen für solche Wagen bisher nicht entwickelt worden, entsprechende Messdaten fehlen. Ein Anhaltspunkt ist die so genannte kritische Steigung, das ist der Wert, ab dem eine Wegführung in Serpentinen effektiver ist als eine geradlinige. Während die kritische Steigung für Fußgänger bei etwa 25% liegt, ist der Wert für Fahrzeuge sehr viel niedriger anzusetzen, zwischen 8 und 16%. Llobera und Sluckin (2007) stellen in ihrer Publikation eine Methode vor, um die kritische Steigung eines einfachen Polynoms 2. Grades zu ermitteln. Umgekehrt kann man diesen Ansatz verwenden, um für eine gegebene kritische Steigung eine entsprechende sehr einfache Kostenfunktion zu konstruieren:
f(s) = 1 + (s / c)²
wobei s die Hangneigung in Prozent und c die vorgegebene kritische Steigung ist.
Wahrscheinlich bestimmten nicht die eher seltenen schnellen Reisewagen sondern die viel häufigeren und schwerfälligeren Fahrzeuge für den Warentransport den Verlauf der Handelsrouten. Bei den bisherigen Studien zur Rekonstruktion von mittelalterlichen Handelswegen im Bergischen Land haben sich einfache Kostenfunktionen mit einer kritischen Steigung von 10 bis 12% bewährt. Abbildung 4 zeigt eine solche Kostenfunktion mit einer kritischen Steigung von 12%. Die Kostenfunktion, die auf den Daten von Minetti et al. (2002) beruht, ist nicht symmetrisch, d.h. dass für Hin- und Rückweg unterschiedliche Kosten anfallen und somit für jede Richtung andere Wege optimal sein könnten. Meist rechnet man jedoch mit einem Mittelwert der Kosten aus beiden Richtungen, so dass die Kostenfunktion symmetrisch wird. Dies ist insbesondere in Zusammenhang mit den Umfeldberechnungen sinnvoll. Die Polynome 2. Grades, die als Kostenfunktionen für Wagen vorgeschlagen wurden, sind schon aufgrund ihrer Konstruktion symmetrisch.
Mit der Wahl der Kostenfunktion ist das schwierige Kapitel Hangneigung noch nicht beendet. Wichtig ist auch, wie die Hangneigung berechnet wird. Grundlage sind hierbei digitale Geländemodelle (DGM), die Höhenwerte für Punkte in einem regelmäßigen Gitter angeben. In der vorliegenden Publikation wird das ASTER-DGM verwendet, das von der NASA und METI kostenfrei zur Verfügung gestellt wird. Der Abstand zwischen benachbarten Gitterpunkten beträgt ca. 30 m. Ein zu großer Gitterabstand führt zu unrichtigen Hangneigungswerten, insbesondere wenn dadurch wesentliche Geländeformationen nicht ausreichend Berücksichtigung finden. Je größer der Abstand zwischen den Gitterpunkten, desto mehr wird das Relief geglättet. Bei einer Halbierung des Gitterabstandes vervierfacht sich die Zahl der Gitterpunkte und damit in der Regel auch die Rechenzeit für die Ermittlung optimaler Wege.
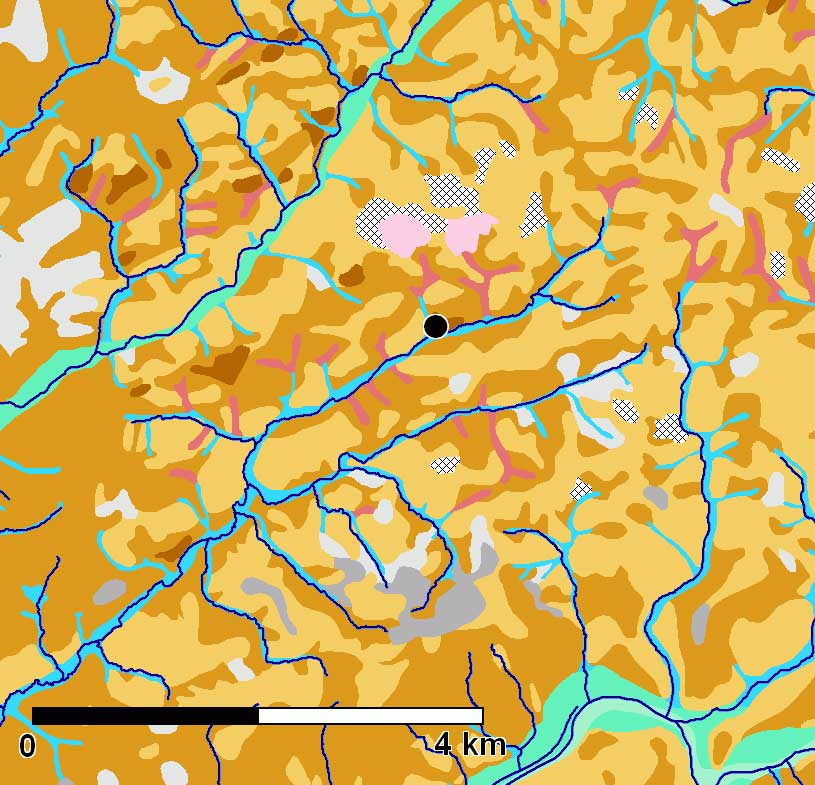
Eine weitere Fehlerquelle sind Messfehler. Bei dem ASTER-DGM hängen diese u.a. davon ab, wie viele Messungen für einen Höhenpunkt vorliegen. Im hier betrachteten Ausschnitt des Bergischen Landes sind dies vier bis 12 Messungen, wobei für die meisten Punkte sieben bis acht solcher Höhenmessungen für das DGM ausgewertet werden konnten. Ab vier Messungen gilt der errechnete Höhenpunkt als recht zuverlässig. Darüber hinaus hat sich die Geländeoberfläche seit dem Mittelalter durch verschiedene natürliche Einflussfaktoren und menschliche Eingriffe verändert. Hierzu zählen Erosionsprozesse, aber auch der Abbau von Rohmaterial. Gerade im Bergischen Land haben u.a. Steinbrüche, Stauseen, Pingen und andere Bergbaurelikte erhebliche Spuren im Geländerelief hinterlassen (s. Abb. 5).
Die Bodenkarte (Abb. 5) zeigt nördlich von Lindlar rosa Flächen, an denen die natürliche Geländeoberfläche durch Abtragung gestört ist. Unmittelbar im Norden grenzen Flächen mit Karomuster an, deren Bodentyp in der Bodenkarte mit »Aufschüttung ohne Bodenentwicklung« bezeichnet wird. Im Umfeld von Lindlar gibt es weitere kleine Gebiete, die mit einer solchen Signatur versehen sind. Nördlich von Lindlar wurde Grauwacke abgebaut, diese Eingriffe sind schon auf der Karte von 1894 (Preußische Neuaufnahme) verzeichnet.
Die Bodenkarte ist nur eine von mehreren Quellen, die solche Landschaftsveränderungen dokumentieren. Die Sammlung dieser Daten ist aufwändig (Gerlach / Herzog 2004), und ein noch höherer Aufwand ist notwendig, um diese Landschaftsveränderungen im digitalen Geländemodell wieder rückgängig zu machen. Daher wurde im Rahmen der hier vorgestellten Berechnungen auf eine Landschaftsrekonstruktion verzichtet, obwohl diese für ein optimales Ergebnis notwendig wäre.
Außerdem gibt es unterschiedliche Methoden, die Hangneigung zu berechnen. Zu unterscheiden ist zwischen der maximalen Hangneigung und der effektiven Steigung. Die maximale Hangneigung gibt in einer positiven Zahl die steilste Richtung an, die in einem Punkt gemessen werden kann, während die effektive Steigung die Bewegungsrichtung berücksichtigt. Abbildung 6 zeigt eine Straße, deren effektive Steigung geringer ist als die der Hangneigung. Bei einem steilen Hang erlaubt die Anlage eines Weges parallel zum Hang, bequem wie auf einer flachen Strecke voran zu kommen. Gerade in Zusammenhang mit der effektiven Steigung gibt es noch einige Probleme bei der Wegeberechnung: So ist es schwierig, die Baukosten für Wege entlang einer Höhenlinie zu schätzen; ohne bauliche Konstruktionen könnte das Fahrzeug kippen, und eine Serpentinenstrecke sollte nicht alle 3 m die Richtung wechseln.
Kombination der Einflussfaktoren
Im vorherigen, sehr langen Abschnitt stand allein die Hangneigung im Mittelpunkt – nicht nur aufgrund der Beliebtheit dieses Kostenfaktors in anderen archäologischen Studien, sondern vor allem aufgrund der Topographie des Bergischen Landes. Häufig verwendete andere Kostenfaktoren sind Bodenbeschaffenheit und Vegetation, Wasser als Transportweg oder als Hindernis sowie Sichtbarkeitsaspekte. Zur Bodenbeschaffenheit gibt es verschiedene physiologische Studien, die entsprechende Multiplikatoren vorschlagen, z.B. den Faktor 1,1 für Trampelpfade und 2 für losen Sand. Aufgrund dieser Studien erscheint es generell sinnvoll, die Faktoren im Kostenmodell durch Multiplikation zu kombinieren.
Ein Rückschluss auf die Vegetation in vergangenen Zeiten ist in der Regel nur durch aufwändige archäobotanische Methoden möglich. Aber ist ein Weg erst mal vorhanden und wird häufig begangen, spielt die Vegetation in der hier betrachteten Region eine recht geringe Rolle, denn das Nachwachsen der Pflanzen wird durch die Reisenden auf dem Weg stark eingeschränkt.
In der Regel wird man mit einem einfachen Kostenmodell anfangen und sukzessive zusätzliche Kostenfaktoren hinzunehmen, bis die errechneten Routen gut mit den Relikten des Altweges zusammen passen. Für das Bergische Land hat sich ein Kostenmodell bewährt, das die Hangneigung mit einem Zusatzfaktor für das Queren von Wasserläufen kombiniert.
Das Testgebiet mit alten Handelsrouten
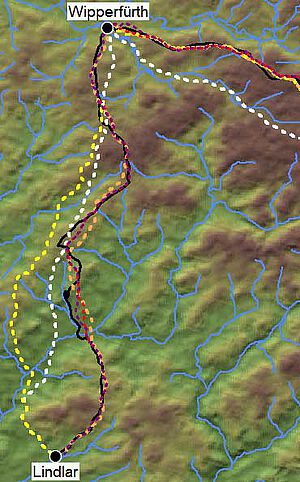
Der so genannte Polizeiweg verbindet Siegburg mit Wipperfürth (Nicke 2001, 115-118), wobei sich im vorliegenden Aufsatz die Wegeberechnungen auf das nördlichste Teilstück ab Lindlar beschränken (für die Strecke im Süden siehe Herzog 2009). Die Ersterwähnungen von Lindlar (1109 n.Chr) und Wipperfürth (1135 n.Chr.) sind für das Bergische Land recht früh. Die Luftlinienentfernung zwischen beiden Orten beträgt 11,0 km, während die bei Nicke beschriebene Route 14,2 km lang ist. Die Höhenwerte auf der Strecke variieren zwischen 180 und 360 m. Abbildung 7 zeigt diese Teilstrecke des Polizeiweges sowie ein kleines Stück der Bergischen Eisenstraße (Nicke 2001, 106-109). Diese beiden Handelsrouten sind in der Karte in schwarz dargestellt.
Rechenergebnisse für den nördlichen Polizeiweg
Die weiß gestrichelten Strecken in Abbildung 7 sind errechnete Routen, die nur auf dem Kostenfaktor Hangneigung basieren, wobei die oben beschriebene Kostenfunktion für Fußgänger zur Anwendung kommt. Es ist leicht zu erkennen, dass diese Rekonstruktionsversuche nur sehr wenig Übereinstimmung mit dem tatsächlichen Streckenverlauf aufweisen. Dies liegt daran, dass die Wasserläufe bei der Berechnung keine Berücksichtigung fanden. Im Mittelalter vermieden die Wege im Bergischen Land Bachquerungen: die breiten Bach- und Flusstäler sind sehr feucht, und die meisten anderen Bachtäler sind tief in das Gelände eingeschnitten, erfordern also einen steilen Ab- und Wiederanstieg. Nur durch entsprechende Baumaßnahmen ist zu verhindern, dass Wege in solchen Bachtälern durch zu viel Schlamm unpassierbar werden. Auch die Kippgefahr bei Streckenführung am steilen Hang ist nur durch Konstruktionsarbeiten zu verringern. Solche Eingriffe in die Landschaft waren jedoch in dieser Region im Mittelalter recht selten, lediglich befestigte Furten und Brücken sind an einigen Stellen nachgewiesen (Nicke 2001, 7-13).
Deshalb wurde das Kostenmodell so angepasst, dass Bach- und Flusstäler mit höheren Kostenfaktoren versehen sind. Die gelb gestrichelten Strecken in Abbildung 7 sind das Ergebnis eines solchen Kostenmodells, das den Faktor 10 für breite (mehr als 3 m) und 5 für schmalere Wasserläufe vorsieht. Doch erst die Erhöhung des Kostenfaktors für kleine Wasserläufe auf 10 (orange gestrichelte Linien) ergibt eine bessere Annäherung an den von Nicke beschriebenen Polizeiweg, während sich das Ergebnis für das hier betrachtete Teilstück der Bergischen Eisenstraße kaum verändert. Auch bei der Nutscheid-Straße (Herzog 2010) konnte gezeigt werden, dass zur erfolgreichen Rekonstruktion der Altstraße ein hoher Kostenfaktor für die kleineren Wasserläufe notwendig ist.
Doch selbst die mit Kostenfaktor 10 für alle Wasserläufe errechneten Routen stimmen streckenweise nicht mit den bekannten Altwegen überein. Bei der Überprüfung zeigte sich, dass das für die Berechnung verwendete Gewässernetz kurze Bäche von etwa 1 km Länge nicht einschließt. Aber die meisten Altwege vermeiden auch solche Wasserläufe. Bei den Wasserläufen in breiten Tälern gibt es zusätzlich das Problem, dass sich Flussmäander schon seit dem Kartenstand von 1848 verändert haben, sowohl durch natürliche Prozesse als auch durch menschliche Eingriffe. Zunächst wurde versucht, die modernen Daten für das Gewässernetz so zu modifizieren, dass sie mit dem Kartenstand von 1848 übereinstimmen. Doch ist dies recht aufwändig, unter anderem weil die kleinen Bäche oft schwer auf dieser Altkarte zu erkennen sind.
Es erwies sich als effektiver, auf die Bodenkarte zurückzugreifen. Im Bergischen Land befinden sich die Wasserläufe auf Gleyböden (türkisfarbene Flächen in Abb. 5 und 8), wobei Auenbereiche mäandrierender Flüsse als breite Gleystreifen auf der Bodenkarte zu erkennen sind. Abbildung 8 zeigt oberhalb der roten Trennlinie die Wasserläufe in mittelblau, die auf der Altkarte von 1848 verzeichnet sind, und darüber das moderne Gewässernetz in dunkelblau. Deutlich erkennbar ist das breite Gleyband der Wupper, das sowohl die Mäander des Flusses aus dem Jahr 1848 als auch den begradigten heutigen Flussverlauf einschließt. Alle in der Altkarte verzeichneten Wasserläufe befinden sich in Gleyzonen. In anderen feuchten Tälern ist kein Bach kartiert – aber auch diese Gleyzonen wurden von Altwegen gemieden.
Für die Wegeberechnungen ist es notwendig, die Gleyflächen auf der Bodenkarte mit einer kleinen Pufferzone von 20 m zu umgeben, sonst könnten sehr schmale Gleybänder durch einen Einzelschritt des errechneten Weges einfach übersprungen werden. Die rot gestrichelten Routen in Abbildung 7 sind mit der Kostenfunktion für Fußgänger und mit einem Kostenfaktor von 10 für Gleyzonen errechnet. Auch die lila gestrichelten Strecken berücksichtigen die Gleyzonen, doch wurde in diesem Fall die Kostenfunktion mit einer kritischen Steigung von 12% verwendet.
Auswertung der Rechenergebnisse
Das Beispiel in Abbildung 7 zeigt sehr deutlich, dass das Kostenmodell auf einer recht breiten Basis aufgestellt werden sollte. Denn für das hier gezeigte Teilstück der Bergischen Eisenstraße liefern alle Kostenmodelle, die das Gewässernetz einbeziehen, gute Ergebnisse – doch ist diese Beobachtung nicht auf den Polizeiweg zwischen Lindlar und Wipperfürth übertragbar. Aufgrund der bisherigen Experimente nicht nur für den Polizeiweg, sondern auch für andere Altwege im Bergischen Land wie die Zeitstraße, den Heerweg, die Brüderstraße und die Bergische Eisenstraße ist das Kostenmodell am besten geeignet, das auf den Gleyzonen der Bodenkarte und einer Kostenfunktion mit einer kritischen Hangneigung von zehn bis zwölf Prozent basiert.
Es ist erstaunlich, dass schon dieses einfache Modell trotz der verhältnismäßig groben und nicht immer exakten topographischen Daten recht gute Anpassungen an den historischen Wegeverlauf liefert. Eine weitere Verbesserung des Rechenergebnisses ist dadurch zu erzielen, dass man bekannte Furten und Brücken im Kostenmodell berücksichtigt. In Abbildung 7 ist zu sehen, dass sich die errechneten Wege und die Altstraße nördlich von Lindlar bei Querung eines Wasserlaufs trennen. Nach Modifikation des Kostenmodells durch Einbau einer Zone mit geringeren Kosten am vermuteten Ort der Brücke oder Furt kann hier voraussichtlich ein größere Übereinstimmung mit der Altstraße erreicht werden.
Eine solche Vorgehensweise führte bei der Rekonstruktion der Altwege durch Wipperfürth zu guten Ergebnissen – wobei Wipperfürth ja schon im Namen anzeigt, wie wichtig die Furt durch die Wupper für die Entstehungsgeschichte der ältesten bergischen Stadt war (Nicke 2001, 204). Deshalb wurden zwei kostengünstige Wupperübergänge bei Wipperfürth in das Modell aufgenommen, deren Lage mit den Brücken auf der Karte von 1848 übereinstimmt.
Die Umfeldanalysen für Lindlar und Wipperfürth
Das oben vorgestellte Kostenmodell bildet die Grundlage für die Umfeldberechnungen in Abbildung 2, die hier als Abbildung 9 noch einmal gezeigt wird. In dieser Abbildung entspricht die innere, rote Linie einem Umfeld von 1 km auf ebenem, trockenen Gelände, der Grenzwert für die äußere, hellgelbe Linie liegt bei 5 km. Bei beiden Siedlungspunkten beeinflussen die Wasserläufe die Form der Umfelder erheblich. So ist das 1-km-Umfeld von Wipperfürth eher oval als rund. Der zentrale Punkt, der im östlichen Bereich des Marktplatzes gewählt wurde, liegt nicht in der Mitte des inneren Umfeldes sondern im Norden. Die Wupper bildet hier eine natürliche Grenze, aber auch der Weinbach im Westen sowie der Gaulbach im Osten formen das 1-km-Umfeld.
Dieses innere Umfeld hat eine Fläche von 48 Hektar, das 5-km-Umfeld umschließt 2216 Hektar. Das 1-km-Umfeld von Lindlar wird von dem Wasserlauf der Lennefe quasi eingeschnürt. Eine solche Einschnürung ist auch beim 2-km-Umfeld noch deutlich erkennbar. Das kleinste Umfeld ist mit 99 Hektar ziemlich genau doppelt so groß wie das innerste Umfeld von Wipperfürth, das äußerste ist mit 2666 Hektar jedoch nur um etwa 20% größer als das entsprechende Umfeld von Wipperfürth. Es sei an dieser Stelle noch einmal darauf hingewiesen, dass diese Berechnungen auf der Grundlage von modernen Geländedaten erfolgten, so dass insbesondere die Ergebnisse für Lindlar nur mit Vorsicht ausgewertet werden können, da sich einige Abbaugebiete in der Nähe der Siedlung befinden.
Abbildung 9 zeigt verschiedene Umfeldradien für die beiden betrachteten Siedlungen. Doch welcher Radius ist der Richtige? Für Bauernkulturen werden häufig Umfelder mit einem Radius von 5 km betrachtet bzw. einer Gehzeit von 60 Minuten, doch in Mitteleuropa kommen auch sehr kleine Radien von 750 m zur Anwendung (Zimmermann et al. 2009; Posluschny 2010). Orientiert man sich an den Regelabständen, die für die räumliche Verteilung von frühmittelalterlichen Siedlungen am Niederrhein bzw. für die Kirchen des Liber Valoris im 13. Jahrhundert ermittelt wurden (Siegmund 2009), ergeben sich andere Werte: Demnach weisen frühmittelalterliche Fundstellen typischerweise Entfernungen zwischen 2,25 und 3,25 km auf, während der Abstand der Kirchen um 1300 meist zwischen 3,25 und 4,75 km liegt.
Da die Landschaft am Niederrhein vergleichsweise flach ist, also die Wegekosten wenig variieren, sind diese Abstände gute Schätzwerte für Umfelddurchmesser. Es kann somit keine allgemeine Empfehlung für die Wahl der Umfeldgröße gegeben werden. Diese hängt von der archäologischen Fragestellung und der Zeitstufe der betrachteten Fundplätze ab.
Erreichbarkeit
Im vorherigen Abschnitt wurde die Wahl der Umfeldgröße diskutiert. Tatsächlich ist eher eine fließende Grenze zu erwarten, denn in vielen Fällen verringert sich die Intensität der Nutzung einer Fläche mit zunehmendem Abstand von der zugehörigen Siedlungsstelle. Das heißt, dass die inneren Umfelder wichtiger sind als die äußeren. Diese Idee ist die Basis eines Modells, mit dem Erreichbarkeit errechnet werden kann. Im einfachsten Fall gilt es punktförmige Ziele wie Rohstoffquellen zu erreichen. Dann kann man Umfelder berechnen, die für jeden Punkt im Umfeld angeben, mit welchem Aufwand der zentrale Punkt zu erreichen ist. Durch eine Gewichtung ist es zusätzlich möglich, der Qualität oder der Ergiebigkeit der Rohstoffquelle Rechnung zu tragen.
Wenn sich die Umfelder mehrerer Rohstoffquellen überlappen, ist das einfachste Modell, jeden Punkt eindeutig der jeweils am besten zu erreichenden Quelle zuzuordnen. Somit entsteht eine Karte, bei der sich die Einzugsbereiche der Rohstoffquellen nicht überschneiden. Bei archäologischen Fundstellen ist jedoch häufig Material aus mehreren Quellen nachweisbar. Dann ist ein Modell sinnvoller, das in der Überlappungszone die Erreichbarkeitswerte kombiniert (Herzog 2011).
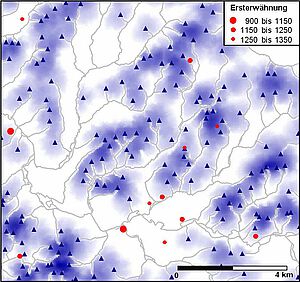
Abbildung 10 ist ein Beispiel für eine solche Erreichbarkeitskarte. Blaue Dreiecke markieren Quellen, d.h. Endpunkte von Wasserläufen, die auf der Altkarte von 1848 verzeichnet sind. Die Wasserläufe sind als graue Linien dargestellt. Für jede einzelne Quelle wurde ein Umfeld mit einem Radius errechnet, der dem Aufwand für die Bewältigung einer flachen Strecke von 1 km entspricht. Die Erreichbarkeit der Quelle ist am Ort der Quelle am höchsten und sinkt mit zunehmendem Abstand von der Quelle. Nach dem hier gewählten Modell werden die Erreichbarkeitswerte in den Überschneidungszonen mehrerer Quellenumfelder addiert. Deshalb ist die Karte dort intensiv blau gefärbt, wo mehrere Quellen dicht beieinander liegen. An weißen Flecken übersteigt der Aufwand zur nächsten Quelle denjenigen, der für eine flache Strecke von 1 km benötigt wird. Rote Punkte markieren Siedlungen, deren Ersterwähnung vor 1350 erfolgte (Pampus 1998).
Die beiden frühesten Siedlungen im Kartenausschnitt sind Hückeswagen (Ersterwähnung: 1085) am linken Kartenrand und Wipperfürth in der Südhälfte der Karte. Beide Siedlungen liegen an der Wupper, wobei sich Wipperfürth nicht im Umfeld von Quellen befindet. Sicherlich ist die Kartierung der Quellen aufgrund der Altkarte von 1848 nicht optimal und die Zahl der betrachteten Siedlungen zu klein, um aus dieser Karte generelle Aussagen über das mittelalterliche Siedlungsmuster im Bergischen Land ableiten zu können. Es geht bei diesem Beispiel vielmehr darum, eine Methode zur Gewinnung solcher Aussagen vorzustellen bzw. bisher bekannte Verfahren zu verbessern.
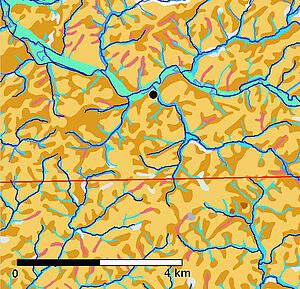
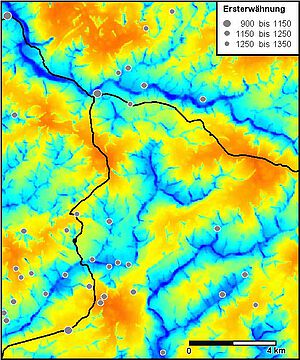
Abbildung 11 zeigt eine generelle Erreichbarkeitskarte, im Kartenausschnitt verläuft der Polizeiweg in der westlichen Hälfte und trifft in Wipperfürth auf die Bergische Eisenstraße, die die Wupper in Wipperfürth quert. Orange-farbige Bereiche sind auf dem Landweg gut, dunkelblaue Flächen vergleichsweise mühsam zu erreichen. Grundlage für die Berechnung einer solchen Karte ist ein gleichmäßiges Raster von Punkten, die im Rechenverfahren als Rohstoffquellen betrachtet werden. In einer topographisch unstrukturierten Landschaft sollten all diese Rohstoffquellen gleich gut zu erreichen sein, so dass eine einheitlich gefärbte generelle Erreichbarkeitskarte entsteht.
Doch in Abbildung 11 sind deutliche Unterschiede in Bezug auf die generelle Erreichbarkeit zu sehen. Zu erwarten ist, dass die alten Handelsrouten in den Zonen hoher Erreichbarkeit verlaufen. Dies trifft sowohl für den Polizeiweg als auch für die Bergische Eisenstraße zu – jedenfalls im Bereich südöstlich von Wipperfürth. Nordwestlich von Wipperfürth durchquert die Eisenstraße eine große Zone mit niedrigen Erreichbarkeitswerten. Insgesamt orientiert sich die Bergische Eisenstraße im Kartenausschnitt sehr stark an der Wupper. Es könnte sein, dass der Flusstransport auf der Wupper eine parallele Straße erforderte oder entstehen ließ, wobei Zonen niedriger Erreichbarkeit in Kauf genommen wurden.
Die frühen Siedlungen bis 1350 liegen vor allem im südwestlichen Bereich in Zonen hoher Erreichbarkeit. Doch in Abbildung 11 sind auch viele auf dem Landweg schwer zu erreichende Siedlungen verzeichnet, meist in unmittelbarer Nähe zu einem Wasserlauf. Dies legt die Vermutung nahe, dass insbesondere die breiteren Wasserläufe wie Wupper und Sülz eine wichtige Rolle in der mittelalterlichen Besiedlungsgeschichte des Bergischen Landes spielen.
Weitere Rechenansätze
Die hier vorgestellten Methoden bilden die Grundlage für weitere landschaftsarchäologische Forschungsansätze: So können auch die Nebenwege zu bekannten Handelsrouten rekonstruiert werden (Herzog 2010b). In der Regel betrachtet man nur Umfelder für einzelne Punkte, doch besteht auch die Möglichkeit, Umfelder von Linien zu berechnen. Dies ist für eine Archäoprognose wichtig, bei der der Zugang zum nächstgelegenen Gewässer eine Rolle spielt (z.B. Münch 2003). In vielen bisherigen Prognosemodellen bilden Pufferzonen um einen Wasserlauf die Basis für eine solche Berechnung, wobei nur der Abstand auf der Karte, nicht aber der tatsächlich benötigte Aufwand berücksichtigt wird.
Weiterhin erlauben die hier diskutierten Verfahren, Gebiete sinnvoll abzugrenzen. So kann man Fürstensitzen Territorien zuordnen, indem man sie im Rechenverfahren wie Rohstoffquellen behandelt, und dann jeden Punkt der Karte dem nächsten Fürstensitz zuordnet. Eine andere Möglichkeit besteht darin, die Umfelder von Siedlungen zu kombinieren, ähnlich wie in Abbildung 10 die Umfelder von Quellen. In diesem Modell sind Zonen hoher Erreichbarkeit mit den Siedlungsgebieten identisch.
Zusammenfassung
Die alten Handelsrouten im Bergischen Land sind Zeugnisse der Bewegungsmuster in früherer Zeit. Ist der Verlauf von Handelsrouten mit Hilfe eines Kostenmodells gut rekonstruierbar, so kann dieses als Grundlage für weitere landschaftsarchäologische Analysen dienen, die die Kenntnis der Bewegungsmuster voraussetzen. Zu nennen ist in diesem Zusammenhang nicht nur die Berechnung von Umfeldern für Siedlungen oder Wasserläufe, sondern auch Erreichbarkeitskarten und die sinnvolle Abgrenzung von Gebieten auf der Grundlage von Punktdaten wie Siedlungsstellen oder Fürstensitze.
Literatur
- Barbe, F., 2007: Karolingische Fernwege in Hessen und Westfalen. Etappenstationen und Straßenfesten an der "Nordstraße". Magister-Hausarbeit im Fach Vor- und Frühgeschichte. Phillips-Universität Marburg.
- Eichfeld, I., 2005: Die vorrömische Eisenzeit im Landkreis Rotenburg (Wümme). Eine landschaftsarchäologische Untersuchung mit Hilfe von GIS. Arch. Ber. Landkr. Rotenburg (Wümme) 12 (Oldenburg 2005).
- Gerlach, R. / Herzog, I., 2004: „Achtung: Löcher in der Landschaft!" Wie ein archäologisches Problem mit Hilfe von Karten und digitalen Geländemodellen eingegrenzt werden kann. In: Denkmäler 3D. Erfassung – Verwaltung – Analyse – Präsentation. VDV-Schriftenreihe Bd. 23, 2004, 54-59.
- Herzog, I., 2009: Berechnung von optimalen Wegen am Beispiel der Zeitstraße. Arch. Inf. 31 (1&2) 2008 (2009), 87-96.
- Herzog, I., 2010a: Die Nutscheidstraße – ein optimaler Naturweg. Arch. Rheinland 2009 (2010), 24-26.
- Herzog, I, 2010b: Die Nutscheidstraße – Ausgangspunkt für die Besiedlung? Arch. Rheinland 2009 (2010), 26-28.
- Herzog, I., 2011: Erreichbarkeit im Bergischen Land. Arch. Rheinland 2010 (2011), 29-31.
- Llobera, M. / Sluckin, T.J., 2007: Zigzagging: Theoretical insights on climbing strategies. Journal of Theoretical Biology 249, 206-217.
- Minetti, A.E. / Moia, Ch. / Roi, G.S. / Susta, D. / Ferretti, G., 2002: Energy cost of walking and running at extreme uphill and downhill slopes. Journal of Applied Physiology 93, 1039-1046.
- Münch, U., 2003: The Research Project „Archäoprognose Brandenburg" - Aims and Concepts. In: Kunow, J. / Müller, J. (Hrsg.), Archäoprognose Brandenburg I, Forschungen zur Archäologie im Land Brandenburg 8, 171-178.
- Nicke, H., 2001: Vergessene Wege. Das historische Fernwegenetz zwischen Rhein, Weser, Hellweg und Westerwald, seine Schutzanlagen und Knotenpunkte (Nümbrecht 2001).
- Pampus, K., 1998: Urkundliche Erstnennungen oberbergischer Orte. Beiträge zur Oberbergischen Geschichte. Sonderband (Gummersbach 1998).
- Polla, S., 2009: GIS-basierte Modellierung der Strecken des Stradiasmos. In: Graßhoff G. / Mittenhuber F. (Hrsg.), Untersuchungen zum Stadiasmos von Patara: Modellierung und Analyse eines antiken geographischen Streckennetzes, Bern Studies in the History and Philosophy of Science, Bern Studies 9, 123-147.
- Posluschny, A., 2010: „Fürstensitze", Zentralität und Hinterland – Erste Aspekte einer Projektsynthese aus Sicht des Projektes „Fürstensitze" & Umland. In: D. Krausse (Hrsg.), „Fürstensitze" und Zentralorte der frühen Kelten. Abschlusskolloquium des DFG-Schwerpunktprogramms 1171 in Stuttgart, 12.–15. Oktober 2009 (Stuttgart 2010) 359–374.
- Siegmund, F., 2009: Archäologische Beiträge zur Geschichte des frühen Mittelalters im Raum zwischen Niers und Kendel. In: Weeze und der Raum an Niers und Kendel im Mittelalter. Weezer Archiv, Schriftenreihe der Gemeinde Weeze 3 (Weeze 2009) 136-144.
- Zimmermann, A. / Wendt, K. P. / Frank, Th. / Hilpert, J., 2009: Landscape Archaeology in Central Europe. Proceedings of the Prehistoric Society 75,1–53.